《序》
夫高而大者莫大于天;厚而广者莫广于地。体恢洪而廓落,形修广而幽清,可以玄象课其进退,然而宏远不可指掌也。可以晷仪验其长短,然其巨阔不可度量也。虽穷神知化不能极其妙,探𦣱索隐不能尽其微,是以诡异之说出,则两端之理生,遂有浑天、盖天,兼而并之。故能弥纶天地之道,有以见天地之𦣱,则浑天有灵宪之文,盖天有周髀之法,累代存之,官司是掌,所以钦若昊天,恭授民时。爽以暗蔽,才学浅昧,隣高山之仰止,慕景行之轨辙,负薪馀日,聊观《周髀》。其旨约而远,其言曲而中,将恐废替,濡滞不通,使谈天者无所取则,辄依经为图,诚冀颓毁重仞之墙,披露堂室之奥,庶博物君子,时逈思焉。
《卷上》
昔者周公问于商高曰:窃闻乎大夫善数也,请问古者包牺立周天历度。夫天不可阶而升,地不可得尺寸而度。请问数安从出?
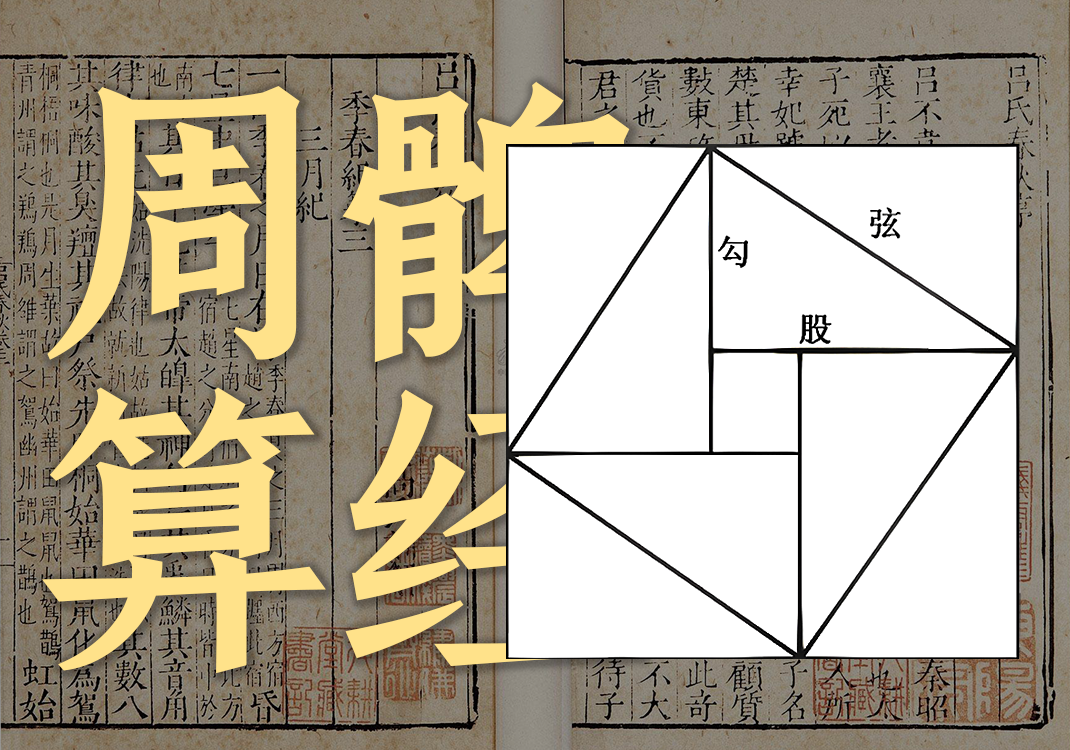
商高曰:数之法,出于圆方。圆出于方,方出于矩。矩出于九九八十一。故折矩,以为句广三,股修四,径隅五。既方之外,半其一矩。环而共盘,得成三、四、五。两矩共长二十有五,是谓积矩。故禹之所以治天下者此数之所生也。
句股圆方图:
![图片[1]-《周髀算经》原文-善米](https://shanmi.site/wp-content/uploads/2024/11/图片1-1.png)
右图:
![图片[2]-《周髀算经》原文-善米](https://shanmi.site/wp-content/uploads/2024/11/图片2-1.png)
左图:
![图片[3]-《周髀算经》原文-善米](https://shanmi.site/wp-content/uploads/2024/11/图片3-1.png)
周公曰:大哉言数!请问用矩之道?
商高曰:平矩以正绳,偃矩以望高,覆矩以测深,卧矩以知远,环矩以为圆,合矩以为方。方属地,圆属天,天圆地方。方数为典,以方出圆。笠以写天。天青黑,地黄赤。天数之为笠也,青黑为表,丹黄为里,以象天地之位。是故知地者智,知天者圣。智出于句,句出于矩。夫矩之于数,其裁制万物,唯所为耳。周公曰:善哉!
昔者荣方问于陈子,曰:今者窃闻夫子之道。知日之高大,光之所照,一日所行,远近之数,人所望见,四极之穷,列星之宿,天地之广袤,夫子之道皆能知之。其信有之乎?陈子曰:然。荣方曰:方虽不省,愿夫子幸而说之。今若方者可教此道邪?陈子曰:然。此皆算术之所及。子之于算,足以知此矣。若诚累思之。
于是荣方归而思之,数日不能得。复见陈子曰:方思之不能得,敢请问之。陈子曰:思之未熟。此亦望远起高之术,而子不能得,则子之于数,未能通类。是智有所不及,而神有所穷。夫道术,言约而用愽者智类之明。问一类而以万事达者谓之知道。今子所学,算数之术,是用智矣,而尚有所难,是子之智类单。夫道术所以难通者既学矣,患其不博。既博矣,患其不习。既习矣,患其不能知。故同术相学,同事相观。此列士之愚智,贤不肖之所分。是故能类以合类,此贤者业精习智之质也。夫学同业而不能入神者此不肖无智而业不能精习。是故算不能精习,吾岂以道隐子哉?固复熟思之。
荣方复归,思之,数日不能得。复见陈子曰:方思之以精熟矣。智有所不及,而神有所穷,知不能得。愿终请说之。陈子曰:复坐,吾语汝。于是荣方复坐而请。陈子说之曰:夏至南万六千里,冬至南十三万五千里,日中立竿测影。此一者天道之数。周髀长八尺,夏至之日晷一尺六寸。髀者股也。正晷者句也。正南千里,句一尺五寸。正北千里,句一尺七寸。日益表南,晷日益长。候句六尺,即取竹,空径一寸,长八尺,捕影而视之,空正掩日,而日应空之孔。由此观之,率八十寸而得径一寸。故以句为首,以髀为股。从髀至日下六万里,而髀无影。从此以上至日,则八万里。若求邪至日者以日下为句,日高为股。句、股各自乘,并而开方除之,得邪至日,从髀所旁至日所十万里。以率率之,八十里得径一里。十万里得径千二百五十里。故曰,日晷径千二百五十里。
日高图:
![图片[4]-《周髀算经》原文-善米](https://shanmi.site/wp-content/uploads/2024/11/图片4-1.png)
法曰:周髀长八尺,句之损益寸千里。故曰:极者天广袤也。今立表高八尺以望极,其句一丈三寸。由此观之,则从周北十万三千里而至极下。荣方曰:周髀者何?
陈子曰:古时天子治周,此数望之从周,故曰周髀。髀者表也。日夏至南万六千里,日冬至南十三万五千里,日中无影。以此观之,从南至夏至之日中十一万九千里。北至其夜半亦然。凡径二十三万八千里。此夏至日道之径也,其周七十一万四千里。从夏至之日中,至冬至之日中十一万九千里。北至极下亦然。则从极南至冬至之日中二十三万八千里。从极北至其夜半亦然。凡径四十七万六千里。此冬至日道径也,其周百四十二万八千里。从春秋分之日中北至极下十七万八千五百里。从极下北至其夜半亦然。凡径三十五万七千里,周一百七万一千里。故曰:月之道常缘宿,日道亦与宿正。南至夏至之日中,北至冬至之夜半,南至冬至之日中,北至夏至之夜半,亦径三十五万七千里,周一百七万一千里。
春分之日夜分以至秋分之日夜分,极下常有日光。秋分之日夜分以至春分之日夜分,极下常无日光。故春秋分之日夜分之时,日所照适至极,阴阳之分等也。冬至、夏至者日道发敛之所生也至,昼夜长短之所极。春秋分者阴阳之修,昼夜之象。昼者阳,夜者阴。春分以至秋分,昼之象。秋分至春分,夜之象。故春秋分之日中光之所照北极下,夜半日光之所照亦南至极。此日夜分之时也。故曰:日照四旁各十六万七千里。
人望所见,远近宜如日光所照。从周所望见北过极六万四千里,南过冬至之日三万二千里。夏至之日中,光南过冬至之日中光四万八千里,南过人所望见一万六千里,北过周十五万一千里,北过极四万八千里。冬至之夜半日光南不至人所见七千里,不至极下七万一千里。夏至之日中与夜半日光九万六千里过极相接。冬至之日中与夜半日光不相及十四万二千里,不至极下七万一千里。夏至之日正东西望,直周东西日下至周五万九千五百九十八里半。冬至之日正东西方不见日。以算求之,日下至周二十一万四千五百五十七里半。凡此数者日道之发敛。冬至、夏至,观律之数,听钟之音。冬至昼,夏至夜。差数及,日光所还观之,四极径八十一万里,周二百四十三万里。
从周至南日照处三十万二千里,周北至日照处五十万八千里,东西各三十九万一千六百八十三里半。周在天中南十万三千里,故东西矩中径二万六千六百三十二里有奇。周北五十万八千里。冬至日十三万五千里。冬至日道径四十七万六千里,周一百四十二万八千里。日光四极当周东西各三十九万一千六百八十三里有奇。
此方圆之法。
万物周事而圆方用焉,大匠造制而规矩设焉,或毁方而为圆,或破圆而为方。方中为圆者谓之圆方,圆中为方者谓之方圆也。
七衡图:
![图片[5]-《周髀算经》原文-善米](https://shanmi.site/wp-content/uploads/2024/11/图片5.png)
凡为此图,以丈为尺,以尺为寸,以寸为分,分一千里。凡用缯方八尺一寸。今用缯方四尺五分,分为二千里。
吕氏曰:凡四海之内,东西二万八千里,南北二万六千里。
凡为日月运行之圆周,七衡周而六间,以当六月节。六月为百八十二日、八分日之五。故日夏至在东井极内衡,日冬至在牵牛极外衡也。衡复更终冬至。故曰:一岁三百六十五日、四分日之一,一岁一内极,一外极。三十日、十六分日之七,月一外极,一内极。是故衡之间万九千八百三十三里、三分里之一,即为百步。欲知次衡径,倍而增内衡之径。二之以增内衡径。次衡放此。
内一衡径二十三万八千里,周七十一万四千里。分为三百六十五度、四分度之一,度得一千九百五十四里二百四十七步、千四百六十一分步之九百三十三。
次二衡径二十七万七千六百六十六里二百步,周八十三万三千里。分里为度,度得二千二百八十里百八十八步、千四百六十一分步之千三百三十二。
次三衡径三十一万七千三百三十三里一百步,周九十五万二千里。分为度,度得二千六百六里百三十步、千四百六十一分步之二百七十。
次四衡径三十五万七千里,周一百七万一千里。分为度,度得二千九百三十二里七十一步、千四百一十分步之六百六十九。
次五衡径三十九万六千六百六十六里二百步,周一百一十九万里。分为度,度得三千二百五十八里十二步、千四百六十一分步之千六十八。
次六衡径四十三万六千三百三十三里一百步,周一百三十万九千里。分为度,度得三千五百八十三里二百五十四步、千四百六十一分步之六。
次七衡径四十七万六千里,周一百四十二万八千里。分为度,得三千九百九里一百九十五步、千四百六十一分步之四百五。
其次,日冬至所北照,过北衡十六万七千里。为径八十一万里,周二百四十三万里。分为三百六十五度四分度之一,度得六千六百五十二里二百九十三步、千四百六十一分步之三百二十七。过此而往者未之或知。或知者或疑其可知,或疑其难知。此言上圣不学而知之。故冬至日晷丈三尺五寸,夏至日晷尺六寸。冬至日晷长,夏至日晷短。日晷损益,寸差千里。故冬至、夏至之日,南北游十一万九千里,四极径八十一万里,周二百四十三万里。分为度,度得六千六百五十二里二百九十三步、千四百六十一分步之三百二十七。此度之相去也。
其南北游,日六百五十一里一百八十二步、一千四百六十一分步之七百九十八。
术曰:置十一万九千里为实,以半岁一百八十二日、八分日之五为法,而通之,得九十五万二千,为实。所得一千四百六十一为法,除之。实如法得一里。不满法者三之,如法得百步。不满法者十之,如法得十步。不满法者十之,如法得一步。不满法者以法命之。
《卷下》
凡日月运行,四极之道。极下者其地高人所居六万里,滂沱四隤而下。天之中央,亦高四旁六万里。故日光外所照径八十一万里,周二百四十三万里。故日运行处极北,北方日中,南方夜半。日在极东,东方日中,西方夜半。日在极南,南方日中,北方夜半。日在极西,西方日中,东方夜半。凡此四方者天地四极四和,昼夜易处,加四时相及。然其阴阳所终,冬至所极,皆若一也。
![图片[6]-《周髀算经》原文-善米](https://shanmi.site/wp-content/uploads/2024/11/图片6.png)
天象盖笠,地法覆盘。天离地八万里,冬至之日虽在外衡,常出极下地上二万里。故日兆月,月光乃出,故成明月。星辰乃得行列。是故秋分以往到冬至,三光之精微,以成其道远。此天地阴阳之性自然也。
欲知北极枢,璇周四极。常以夏至夜半时北极南游所极,冬至夜半时北游所极,冬至日加酉之时西游所极,日加卯之时东游所极。此北极璇玑四游。正北极璇玑之中,正北天之中。正极之所游,冬至日加酉之时,立八尺表,以绳系表颠,希望北极中大星,引绳致地而识之。又到旦,明日加卯之时,复引绳希望之,首及绳致地而识其端,相去二尺三寸。故东西极二万三千里,其两端相去正东西。中折之以指表,正南北。加此时者皆以漏揆度之。此东、西、南、北之时。其绳致地所识,去表丈三寸,故天之中去周十万三千里。何以知其南北极之时?以冬至夜半北游所极也北过天中万一千五百里,以夏至南游所极不及天中万一千五百里。此皆以绳系表颠而希望之,北极至地所识丈一尺四寸半,故去周十二万四千五百里,过天中万一千五百里;其南极至地所识九尺一寸半,故去周九万一千五百里,其南不及天中万一千五百里。此璇玑四极南北过不及之法,东、西、南、北之正勾。
周去极十万三千里。日去人十六万七千里。夏至去周一万六千里。夏至日道径二十三万八千里,周七十一万四千里。春、秋分日道径三十五万七千里,周一百七万一千里。冬至日道径四十七万六千里,周一百四十二万八千里。日光四极八十一万里,周二百四十三万里。从周南三十万二千里。
璇玑径二万三千里,周六万九千里。此阳绝阴彰,故不生万物。其术曰,立正勾定之。以日始出,立表而识其晷。日入,复识其晷。晷之两端相直者正东西也。中折之指表者正南北也。极下不生万物。何以知之?冬至之日去夏至十一万九千里,万物尽死;夏至之日去北极十一万九千里,是以知极下不生万物。北极左右,夏有不释之冰。
春分、秋分,日在中衡。春分以往日益北,五万九千五百里而夏至。秋分以往日益南,五万九千五百里而冬至。中衡去周七万五千五百里。中衡左右冬有不死之草,夏长之类。
此阳彰阴微,故万物不死,五谷一岁再熟。
凡北极之左右,物有朝生暮获。
立二十八宿,以周天历度之法。
术曰:倍正南方,以正勾定之。即平地径二十一步,周六十三步。令其平矩以水正,则位径一百二十一尺七寸五分。因而三之,为三百六十五尺、四分尺之一,以应周天三百六十五度、四分度之一。审定分之,无令有纤微。分度以定,则正督经纬。而四分之一,合各九十一度十六分度之五。于是圆定而正。则立表正南北之中央,以绳系颠,希望牵牛中央星之中。则复望须女之星先至者。如复以表绳希望须女先至,定中。即以一游仪希望牵牛中央星,出中正表西几何度。各如游仪所至之尺,为度数。游在于八尺之上,故知牵牛八度。其次星放此,以尽二十八宿度,则之矣。
立周度者各以其所先至游仪度上。车辐引绳,就中央之正以为毂,则正矣。日所以入,亦以周定之。欲知日之出入,即以三百六十五度、四分度之一而各置二十八宿。以东井夜半中,牵牛之初临子之中。东井出中正表西三十度十六分度之七,而临未之中,牵牛初亦当临丑之中,于是天与地税,乃以置周二十八宿。置以定,乃复置周度之中央立正表。以冬至、夏至之日,以望日始出也,立一游仪于度上,以望中央表之晷。晷参正,则日所出之宿度。日入放此。
牵牛去北极百一十五度千六百九十五里二十一步、千四百六十一分步之八百一十九。
术曰:置外衡去北极枢二十三万八千里,除璇玑万一千五百里。其不除者二十二万六千五百里以为实。以内衡一度数千九百五十四里二百四十七步、千四百六十一分步之九百三十三以为法。实如法得一度。不满法,求里、步。约之合三百得一以为实。以千四百六十一分为法,得一里。不满法者三之,如法得百步。不满法者又上十之,如法得一步。不满法者以法命之。次放此。
娄与角去北极九十一度六百一十里二百六十四步、千四百六十一分步之千二百九十六。
术曰:置中衡去北极枢十七万八千五百里以为实。以内衡一度数为法。实如法得一度。不满法者求里、步。不满法者以法命之。
东井去北极六十六度千四百八十一里一百五十五步、千四百六十一分步之千二百四十五。
术曰:置内衡去北极枢十一万九千里,加璇玑万一千五百里,得十三万五百里以为实。
以内衡一度数为法。实如法得一度。不满法者求里、步。不满者以法命之。
凡八节二十四气,气损益九寸九分、六分分之一。冬至晷长一丈三尺五寸,夏至晷长一尺六寸。问次节损益寸数长短各几何?
冬至晷长一丈三尺五寸,小寒丈二尺五寸,大寒丈一尺五寸一分,立春丈五寸二分,雨水九尺五寸二分,启蛰八尺五寸四分,春分七尺五寸五分,清明六尺五寸五分,谷雨五尺五寸六分,立夏四尺五寸七分,小满三尺五寸八分,芒种二尺五寸九分,夏至一尺六寸,小暑二尺五寸九分,大暑二尺五寸八分,立秋四尺五寸七分,处暑五尺五寸六分,白露六尺五寸五分,秋分七尺五寸五分,寒露八尺五寸四分,霜降九尺五寸三分,立冬丈五寸二分,小雪丈一尺五寸一分,大雪丈二尺五寸。
凡为八节二十四气,气损益九寸九分、六分分之一。冬至、夏至为损益之始。
术曰:置冬至晷,以夏至晷减之,馀为实。以十二为法。实如法得一寸。不满法者十之,以法除之,得一分。不满法者以法命之。月后天十三度、十九分度之七。
术曰:置章月二百三十五,以章岁十九除之,加日行一度,得十三度、十分九度之七。此月一日行之数,即后天之度及分。
小岁月不及故舍三百五十四度、万七千八百六十分度之六千六百一十二。
术曰:置小岁三百五十四日、九百四十分日之三百四十八,以月后天十三度、十九分度之七乘之,为实。又以度分母乘日分母为法。实如法,得积后天四千七百三十七度、万七千八百六十分度之六千六百一十三。以周天三百六十五度、万七千八百六十分度之四千四百六十五除之。其不足除者此月不及故舍之分度数。他皆放此。
大岁月不及故舍十八度、万七千八百六十分度之万一千六百二十八。
术曰:置大岁三百八十三日、九百四十分日之八百四十七。以月后天十三度、十九分度之七乘之为实。又以度分母乘日分母为法。实如法得积后天五千一百三十二度、万七千八百六十分度之二千六百九十八。以周天除之。其不足除者此月不及故舍之分度数。
经岁月不及故舍百三十四度、万七千八百六十分度之万一百里。
术曰:置经岁三百六十五日、九百四十分日之二百三十五,以月后天十三度十九分度之七乘之为实。又以度分母乘日分母为法。实如法,得积后天四千八百八十二度、万七千八百六十分度之万四千五百七十。以周天除之。其不足除者此月不及故舍之分度数。
小月不及故舍二十二度、万七千八百六十分度之七千七百三十五。
术曰:置小月二十九日,以月后天十三度、十九分度之七乘之为实。又以度分母乘日分母为法。实如法得积后天三百八十七度、万七千八百六十分度之万二千二百二十。以周天分除之。其不足除者此月不及故舍之分度数。大月不及故舍三十五度、万七千八百六十分度之万四千三百三十五。
术曰:置大月三十日,以月后天十三度、十九分度之七乘之为实。又以度分母乘日分母为法。实如法得积后天四百一度、万七千八百六十分度之九百四十。以周天除之。其不足除者此月不及故舍之分度数。
经月不及故舍二十九度、万七千八百六十分度之九千四百八十一。
术曰:置经月二十九日、九百四十分日之四百九十九,以月后天十三度、十九分度之七乘之为实。又以度分母乘日分母为法。实如法得积后天三百九十四度、万七千八百六十分度之万三千九百四十六。以周天除之。其不足除者此月不及故舍之分度数。
冬至昼极短,日出辰而入申。阳照三,不覆九。东西相当正南方。夏至昼极长,日出寅而入戌。阳照九,不覆三。东西相当正北方。
日出左而入右,南北行。
故冬至从坎,阳在子,日出巽而入坤,见日光少,故曰寒。夏至从离,阴在午,日出艮而入干,见日光多,故曰暑。日月失度而寒暑相奸。往者诎,来者信也,故屈信相感。故冬至之后日右行,夏至之后日左行。左者往,右者来。故月与日合为一月,日复日为一日,日复星为一岁。外衡冬至,内衡夏至,六气复返,皆谓中气。
阴阳之数,日月之法。十九岁为一章。四章为一蔀,七十六岁。二十蔀为一遂,遂千五百二十岁。三遂为一首,首四千五百六十岁。七首为一极,极三万一千九百二十岁。生数皆终,万物复始。天以更元,作纪历。
何以知天三百六十五度、四分度之一,而日行一度?而月后天十三度、十九分度之七。二十九日、九百四十分日之四百九十九为一月,十二月、十九分月之七为一岁。周天除之。其不足除者如合朔。古者包牺、神农制作为历,度元之始,见三光未如其则。日、月、列星,未有分度。日主昼,月主夜,昼夜为一日。日月俱起建星。月度疾,日度迟。日、月相逐于二十九日、三十日间,而日行天二十九度馀,未有定分。于是三百六十五日南极影长,明日反短。以岁终日影反长,故知之三百六十五日者三,三百六十六日者一。故知一岁三百六十五日、四分日之一,岁终也。月积后天十三周,又与百三十四度馀,无虑后天十三度、十九分度之七,未有定。于是日行天七十六周,月行天千一十六周,及合于建星。置月行后天之数,以日后天之数除之,得一十三度、十九分度之七,则月一日行天之度。复置七十六岁之积月,以七十六岁除之,得十二月、十九分月之七,则一岁之月。
置周天度数,以十二月、十九分月之七除之,得二十九日、九百四十分日之四百九十九,则一月日之数。